Maxima - Using its symbolic math capabilities

Maxima - Using its symbolic math capabilities:

The following table develops progressively more sophisticated uses of Maxima as a symbolic math tool. Remember, you do not need to use or memorize all of this table at once - simply go up to the point that your current needs dictate, and return to this table when they become more extensive.
Note: in the third column some expressions have been typeset for greater ease of reading.

Topic	Discussion	Maxima Input	Maxima Output
Basic typing	Remember, use a semicolon and the enter key to terminate input.	`(2+5/6-sqrt(4))^2;`	`25 -- 36`
Using the previous line	The % symbol tells Maxima to use the result of the previous calculation.	`%+1;`	`61 -- 36`
Using a line by name	Alternatively, you can refer to a result you wish to use by the name of its output line.	`D2+1;`	`97 -- 36`
Numeric evaluation	To tell Maxima to calculate a floating point result, use the float function.	`float(%);`	`2.694444444444445`
Defining a function	To define a function: give it a name, followed by its independent variable in parentheses, followed by the symbols :=, followed by its definition.	`f1(x):=x^2-5*x+6;`	`2 f1(x) := x - 5 x + 6`
Using a function	Once defined, you can use a function in an intuitive way.	`f1(5);`	`6`
Assigning a value to a variable	The : sign assigns a value to a variable.	`a:5;`	`5`
Assigning a value to a variable	The variable assignment will now be used everywhere in place of the variable name.	`f1(a);`	`6`
Defining an equation	The `=` sign defines an equation.	`x=1-b*y;`	`x = 1 - b y`
Solving an equation	An equation can be readily solved for any of its variables, if a simple expression exists.	`solve(%,y);`	`x - 1 [y = - -----] b`
	Another example, yielding both roots of a quadratic.	`solve(x^2+2*x-3=0,x);`	`[x = - 3, x = 1]`
	In order to use any of the results from a solve step, we need to "extract" them from the output list.	`%[2];`	`x = 1`
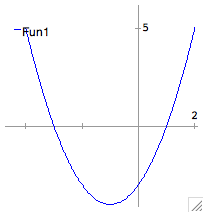
Plotting a function	Let's look at a plot of our function and see that the roots tally. The second argument used by the plot2d function is a list, and is indicated by square brackets ([]). This particular list specifies the x-range of interest.	`plot2d(x^2+2*x-3=0,[x,-4,2]);`
Systems of equations	Maxima can also solve systems of equations, if the equations and variables of interest are presented to it as lists.	`solve([x+3y=3,2x+5*y=5],[x,y]);`	`[[x = 0, y = 1]]`
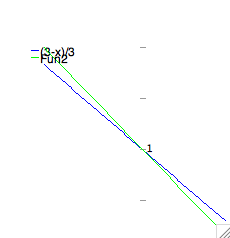
Plotting multiple functions	To plot multiple functions, we use a list of their names as the first argument in the plot2d function. Let's use this feature to check the previous result.	`plot2d([(3-x)/3,(5-2*x)/5],[x,-1,1]);`
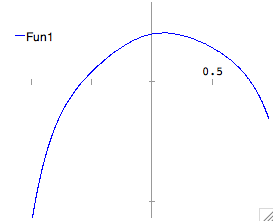
Solving equations numerically	Even when an analytic solution cannot be found, Maxima can in many cases solve the equation numerically. Let's first examine this seventh-order polynomial by plotting it.	`plot2d(x^7-5x^6+4x^4-5*x^2+x+2,[x,-1,1]);`
	We see two roots between -1 and 1. To get their exact values, we load the newton routine, and use it with a guess to the right of the root we wish to get.	`load("newton");`	`/sw/share/maxima/5.9.0rc3/share/numeric/newton.mac`
		`newton(x^7-5x^6+4x^4-5*x^2+x+2,1);`	`8.194213634964119B-1`
	We repeat the process for the second root.	`newton(x^7-5x^6+4x^4-5*x^2+x+2,0);`	`- 5.763042928902195B-1`
Functions of multiple variables	Multivariate functions are defined as before, but separating variables with commas in the definition.	`f2(x,y):=sin(x^2+y^2);`	`2 2 f2(x, y) := SIN(x + y )`
		`f2(1,4);`	`SIN(17)`
		`float(%);`	`- .9613974918795568`
3D Plots	These are created as before, but using the plot3d command, and with separate lists for the ranges of the x and y axes.	`plot3d(f2(x,y),[x,-1,1],[y,-1,1]);`
Factoring Polynomials	Maxima can factor some polynomials.	`factor(x^2+2*x+1);`	`2 (x + 1)`
Expanding Polynomials	Or expand them	`expand(%);`	`2 x + 2 x + 1`
Simplifying Trigonometric expressions	Much the same can be accomplished for trigonometric expressions.	`trigsimp(sin(x)^2+cos(x)^2);`	`1`
Expanding Trigonometric expressions	As with their expansion.	`trigexpand(cos(x+3*y));`
		`trigexpand(%);`
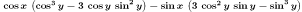		`expand(%)`;
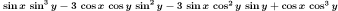Simplifying rational expressions	In many cases, Maxima can simplify rational expressions	`fullratsimp((x^2+2x+1)/(x+1)+1/(4x+3));`
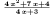Expanding rational expressions	Or expand them.	`ratexpand((x^2-1)/(x+2));`
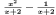Substituting the Results of One Calculation Into Another	We can save ourselves quite a bit of typing by using substitutions. First, we isolate the result we wish to substitute.	`solve(x^2-1=0,x);`	`[x = - 1, x = 1]`
		`%[2];`	`x = 1`
	Then, we perform our substitution	`subst(%,y=3*x-11);`	`y = - 8`
Calculating limits	Let's create an interesting function, and calculate its limit as x approaches 0	`f3(x):=sin(x)/x;`	`SIN(x) f3(x) := ------ x`
		`limit(f3(x),x,0);`	`1`
	To calculate the limit from above, we simply add PLUS (or MINUS from below) to our entry.	`limit(tan(x),x,%PI/2,PLUS);`	`MINF`
		`limit(tan(x),x,%PI/2,MINUS);`	`INF`
Simple Differentiation	We can differentiate any function with respect to a given variable	`diff(cx^2-sin(dx),x);`	`2 c x - d COS(d x)`
Higher Order Differentiation	Higher order differentiation is also readily available.	`diff(x^3,x,3);`	`6`
Simple Integration	We can also perform indefinite integration on a function (assuming a simple closed form for the answer exists and is computable by Maxima).	`integrate(cos(3*x),x);`	`SIN(3 x) -------- 3`
Definite Integration	Or definite integration, if we enumerate the lower and upper limit.	`integrate(cos(3*x),x,0,%PI/2);`	`1 - - 3`
Numeric Integration	In cases where a closed form integral is unavailable, Maxima can compute the result numerically.	`integrate(sin(sin(x)),x,0,1);`
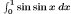Numeric Integration		`romberg(sin(sin(x)),x,0,1);`	`.4306059236425572`
Summation	Summations can be written out.	`sum(1/(n^2),n,1,INF);`
	If desired, they can be evaluated by setting SIMPSUM to TRUE.	`SIMPSUM:TRUE;`	`TRUE`
		`sum(1/(n^2),n,1,INF);`	`2 %PI ---- 6`
Products	Products work in much the same way.	`product(1/(n^2),n,1,10);`	`1 -------------- 13168189440000`
Series Expansion	Series expansions can also be computed. Let's calculate the series expansion of the sine function around x=0, up to the fifth power in x.	`taylor(sin(x),x,0,5);`	`3 5 x x /T/ x - -- + --- + . . . 6 120`
	Since the output of taylor has special properties, we need to convert it into a polynomial.	`trunc(%);`	`3 5 x x x - -- + --- + . . . 6 120`
	We can now compare our series approximation to the original function.	`plot2d([%,sin(x)],[x,0,%PI]);`

We welcome your feedback on this workflow/tutorial - please email us at [email protected]